飯田港・輪島港の再現地震動は，中小地震記録に見かけの震源時間関数を畳み込み等価線形解析¹⁾で引き戻す方法で求めた．見かけの震源時間関数は飯田港・輪島港の最寄りの防災科学技術研究所の強震観測点における記録を再現できるように求めた．

図-1　解析イメージ

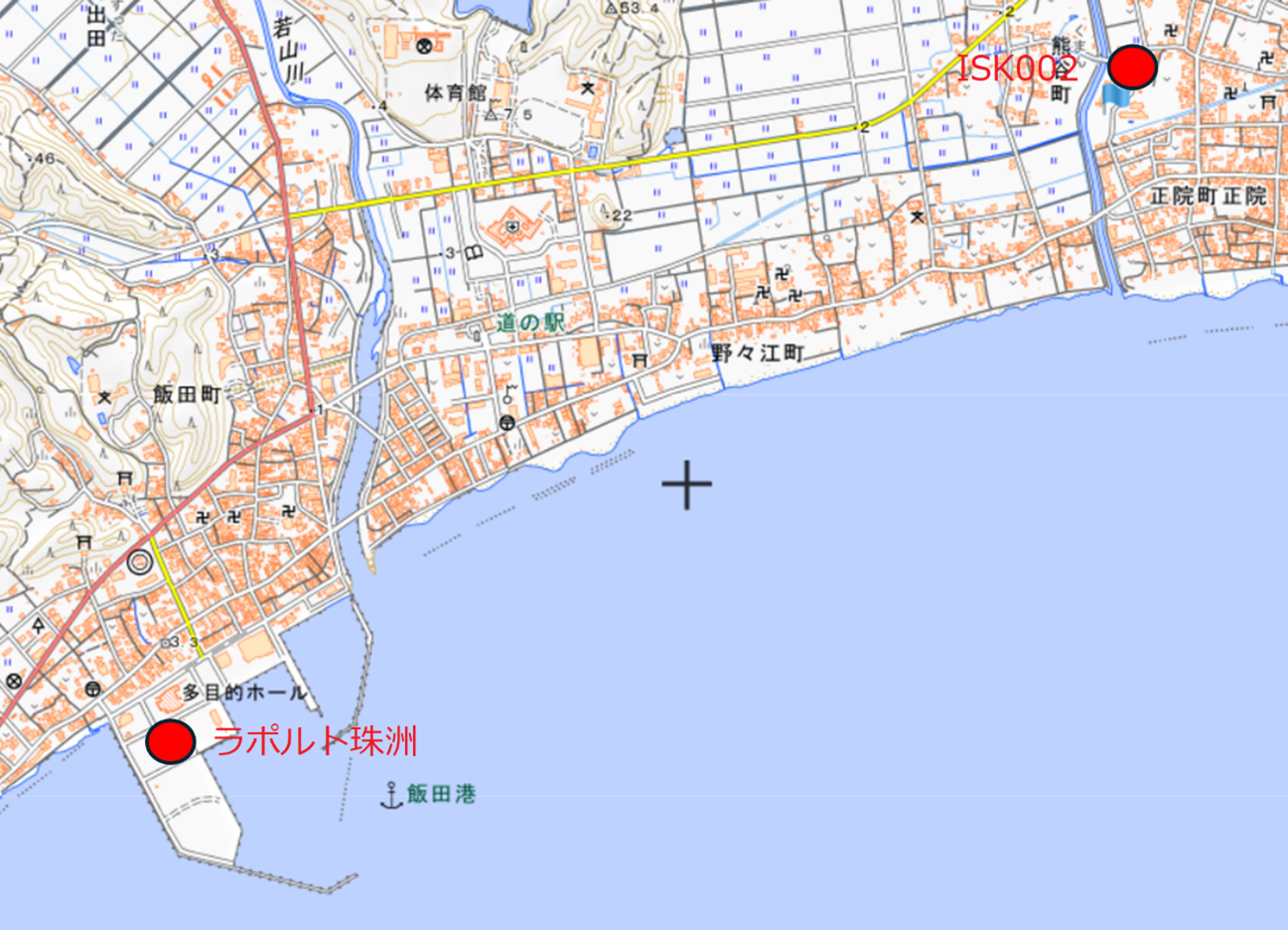
飯田港の場合は，最寄りの防災科学技術研究所の強震観測点はISK002（K-NET正院）であるため（図-2），ISK002における本震記録を再現できるように見かけの震源時間関数を求めた．中小地震記録は，本震記録との位相特性の類似性を考慮し，2月15日15:29の余震（M5.0）の記録を用いた．本震の速度波形を∆t=0.05sでリサンプリングしたデータをv_m (i)，余震の速度波形を∆t=0.05sでリサンプリングしたデータをv_a (i)とし，見かけの震源時間関数w(i)は次式で求めた．N_Sは600とした．これは30秒分の震源時間関数を求めたことになる．

     (1)

本震・余震の発震時刻と震源位置から本震波形におけるS波初動の到来時刻を求め，それに対応するようにi₀を決めたところ，本震波形の最初の部分を表現できない結果となったため，i₀を13秒分だけ前に移した．w(i)を求める際，本震波形の15秒～75秒までのデータを用いた．式(1)を解く際には非負の最小自乗解を求めるためのサブルーチン²⁾を用いた．

式(1)を解く際にEW成分とNS成分を同時にデータとして用いると誤差が生じるが，その誤差は合成波形の過小評価となって表れる．これは，地震動の事後推定を目的とする場合においては不都合であるから，1成分（この場合はEW成分）のみをデータとして用い，得られた見かけの震源時間関数を用いて他の1成分が再現できることを後から確認した．

図-2　飯田港とISK002（K-NET正院）の位置関係

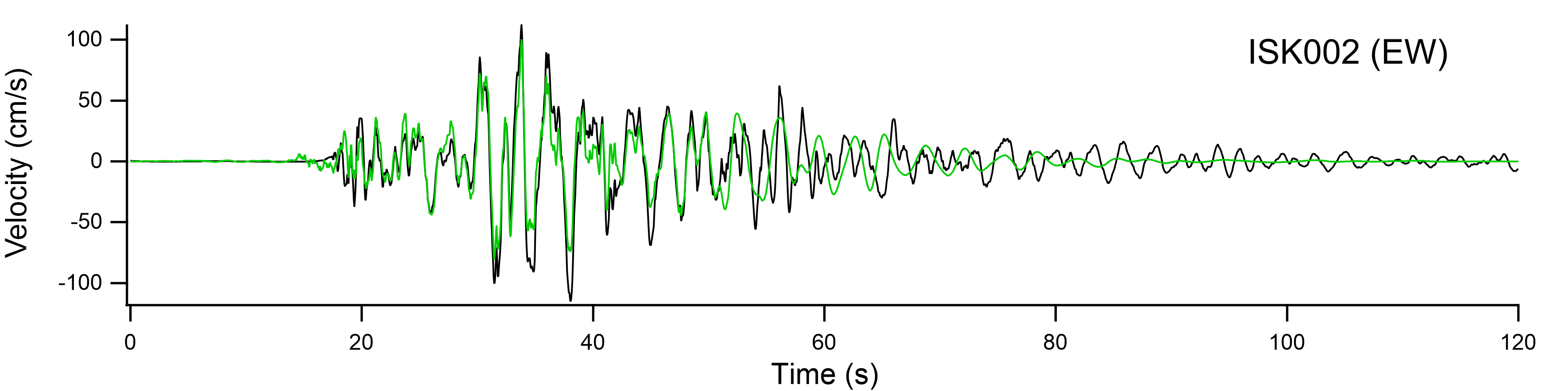
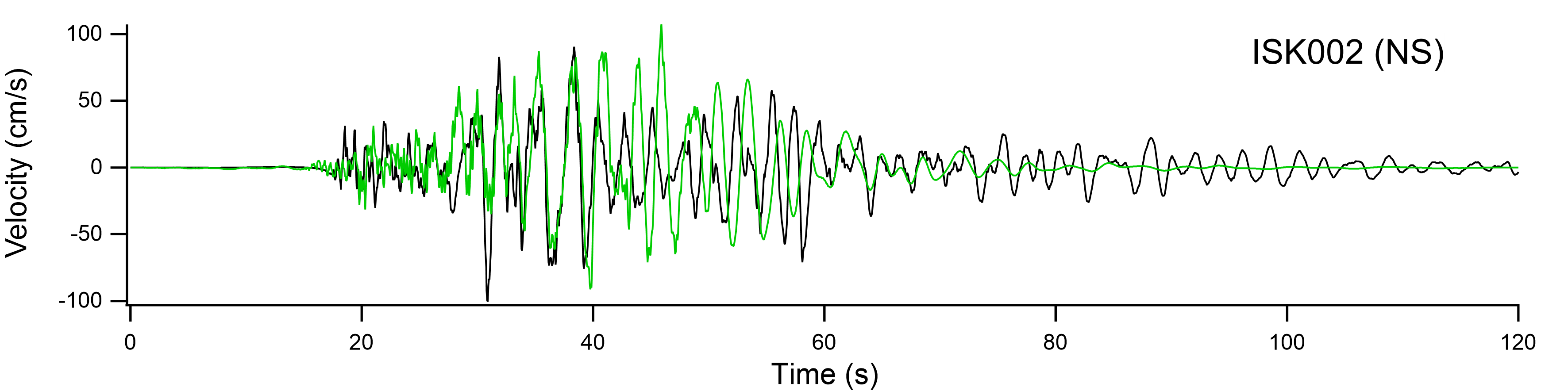
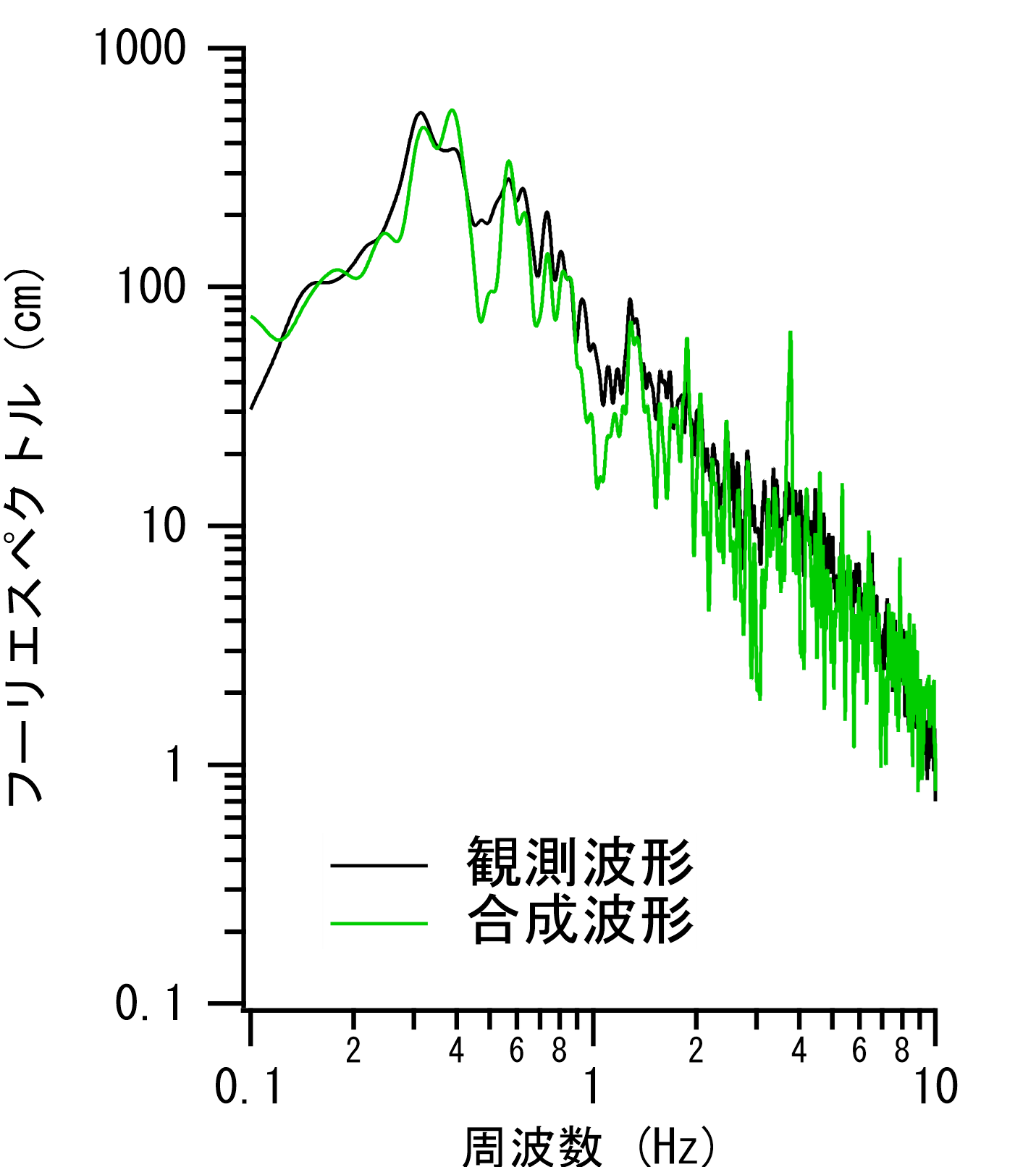
また，ISK002では大振幅の地震動が観測されており，地盤の非線形挙動が生じていたことは明らかである．そこで，これを簡便に表現するため，多重非線形効果を表すパラメタν₁とν₂を用いた．ν₁とν₂は試行錯誤により波形の再現がうまく行くように決めた（ν₁=0.70，ν₂=0.04とした）．他のパラメタを用いた場合は，見かけの震源時間関数を決定する際の誤差が大きくなるか，もしくは，見かけの震源時間関数の決定に用いなかった方の成分の再現がうまく行かない傾向が見られた．

図-3の上段に見かけの震源時間関数の決定に用いた方の成分の再現性を示す．図-3の下段に見かけの震源時間関数の決定に用いなかった方の成分の再現性を示す．見かけの震源時間関数の決定に用いなかった方の成分も合成波形を1秒だけ後ろに動かすと観測波形とよく一致した．図-4に示すようにフーリエスペクトルの再現性も良好である．時間領域の合積は周波数領域のかけ算であるため，図-1の関係を満たす見かけの震源時間関数を求めれば，フーリエスペクトルを良好に再現できることが期待できる．ただし，中小地震記録の水平2成分のフーリエスペクトルに大きな違いがある場合は注意を要する．

図-3　ISK002における本震波形の再現性（緑が合成波形）

図-4　ISK002におけるフーリエスペクトルの再現性（緑が合成波形）

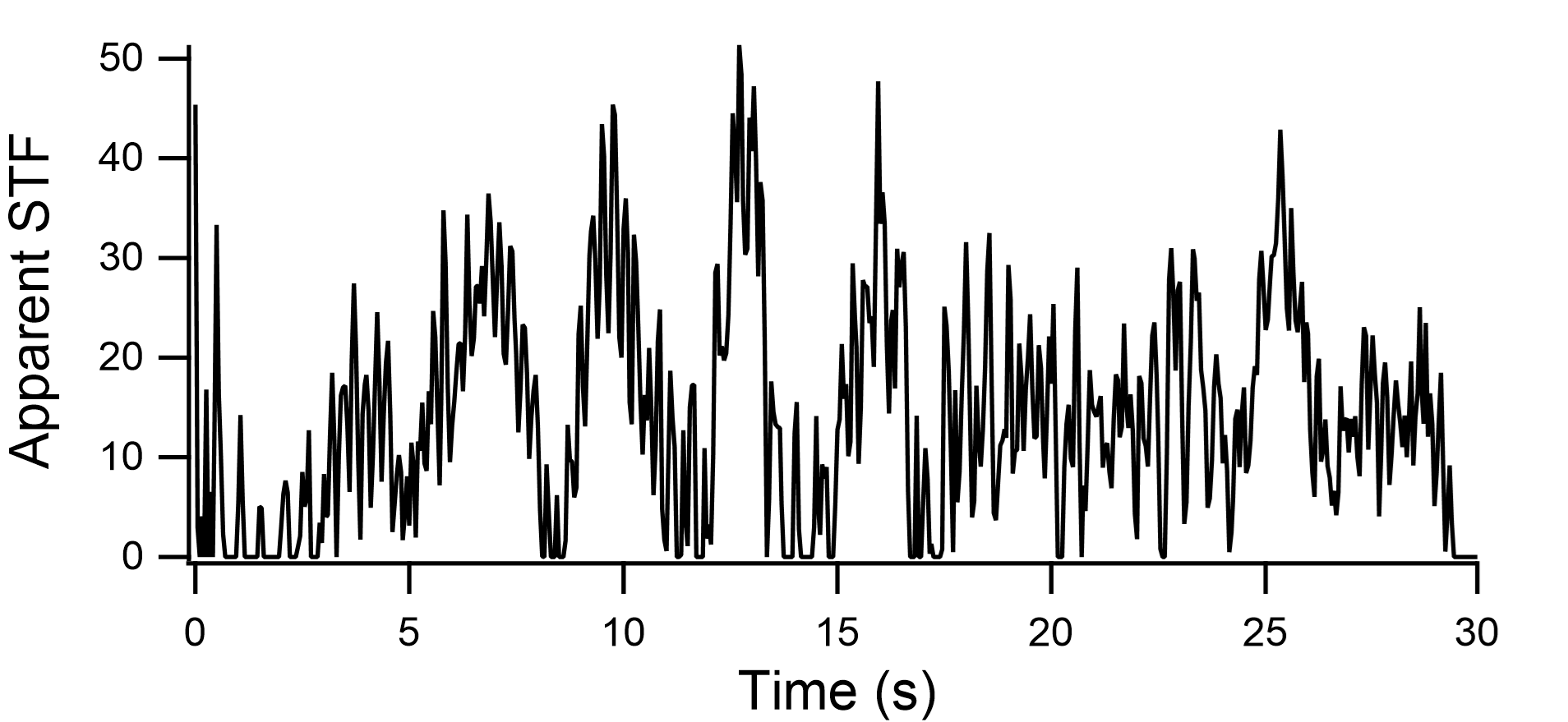
図-5　ISK002における見かけの震源時間関数

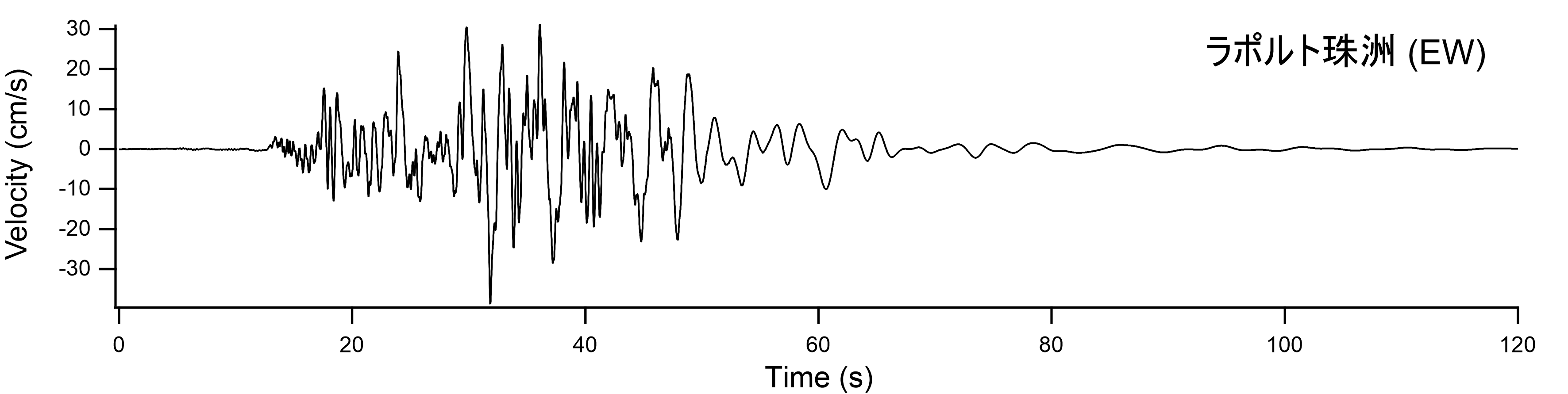
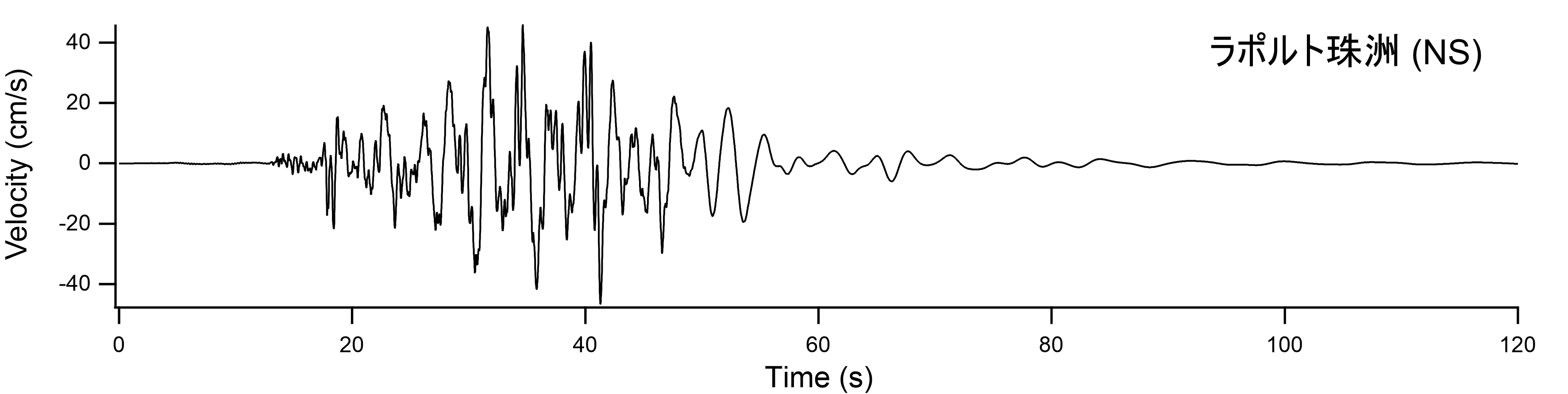
図-6　飯田港（ラポルト珠洲）における再現波（地表における速度波形）

図-5に得られた見かけの震源時間関数を示す．これを用いて飯田港（余震観測を行ったラポルト珠洲）における本震波形を推定した．その際，多重非線形効果を表すパラメタはISK002における波形の再現に用いたのと同じ値（ν₁=0.70，ν₂=0.04）を用いた．飯田港（ラポルト珠洲）における再現波（地表における速度波形）を図-6に示す．PSI値はNS成分が94，EW成分が68となり，ISK002における観測波よりかなり小さくなった．これは，ISK002よりも飯田港（ラポルト珠洲）の方が1Hz以下においてサイト増幅特性が小さい（概ね1/3程度）ためであると考えられる．ここで求まった地震動をL1地震動と同様の地盤モデルで工学的基盤に引き戻したものをエクセルファイルに収録した．なお，ひずみ依存曲線は北澤他³⁾のものを用いた．

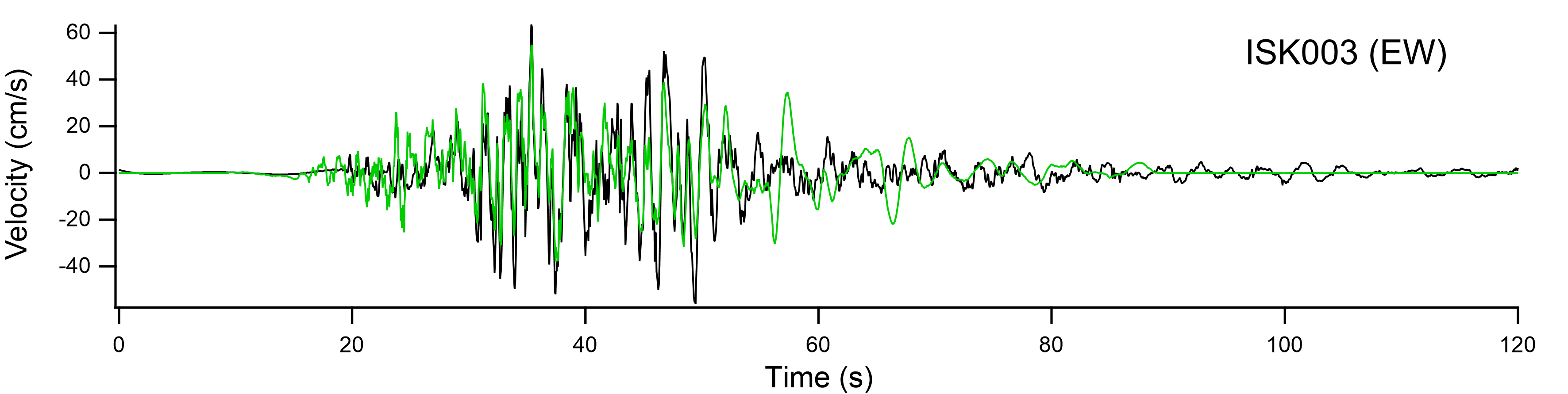
輪島港の場合は，最寄りの防災科学技術研究所の強震観測点はISK003（K-NET輪島）であるため，ISK003における本震記録を再現できるように見かけの震源時間関数を求めた．中小地震記録は，本震記録との位相特性の類似性を考慮し，2月15日15:29の余震（M5.0）の記録を用いた．見かけの震源時間関数w(i)は式(1)で求めた．N_Sは400とした．これは20秒分の震源時間関数を求めたことになる．本震・余震の発震時刻と震源位置から本震波形におけるS波初動の到来時刻を求め，それに対応するようにi₀を決めたところ，本震波形の最初の部分を表現できない結果となったため，i₀を10秒分だけ前に移した．w(i)を求める際，本震波形の25秒～55秒までのデータを用いた．式(1)を解く際には非負の最小自乗解を求めるためのサブルーチン²⁾を用いた．1成分（この場合はEW成分）のみをデータとして用い，得られた見かけの震源時間関数を用いて他の1成分が再現できることを後から確認した．また，ISK003では大振幅の地震動が観測されており，地盤の非線形挙動が生じていたことは明らかである．そこで，これを簡便に表現するため，多重非線形効果を表すパラメタν₁とν₂を用いた．ν₁とν₂は試行錯誤により波形の再現がうまく行くように決めた（ν₁=0.70，ν₂=0.02とした）．他のパラメタを用いた場合は，見かけの震源時間関数を決定する際の誤差が大きくなるか，もしくは，見かけの震源時間関数の決定に用いなかった方の成分の再現がうまく行かない傾向が見られた．ISK003での再現性に関する限り，ν₂の値をもっと大きくすることもできるが，その場合，「輪島港では16:10:46頃にいったん揺れが小さくなったあと16:10:54頃に2回目の大きな揺れがあった」との監視カメラ映像から読み取れる事実と整合しない結果が得られたため，ν₂の値をより大きくすることはしなかった．

図-7の上段に見かけの震源時間関数の決定に用いた方の成分の再現性を示す．図-7の下段に見かけの震源時間関数の決定に用いなかった方の成分の再現性を示す．観測波形の再現性は良好である．また，図-8に示すようにフーリエスペクトルの再現性も良好である．

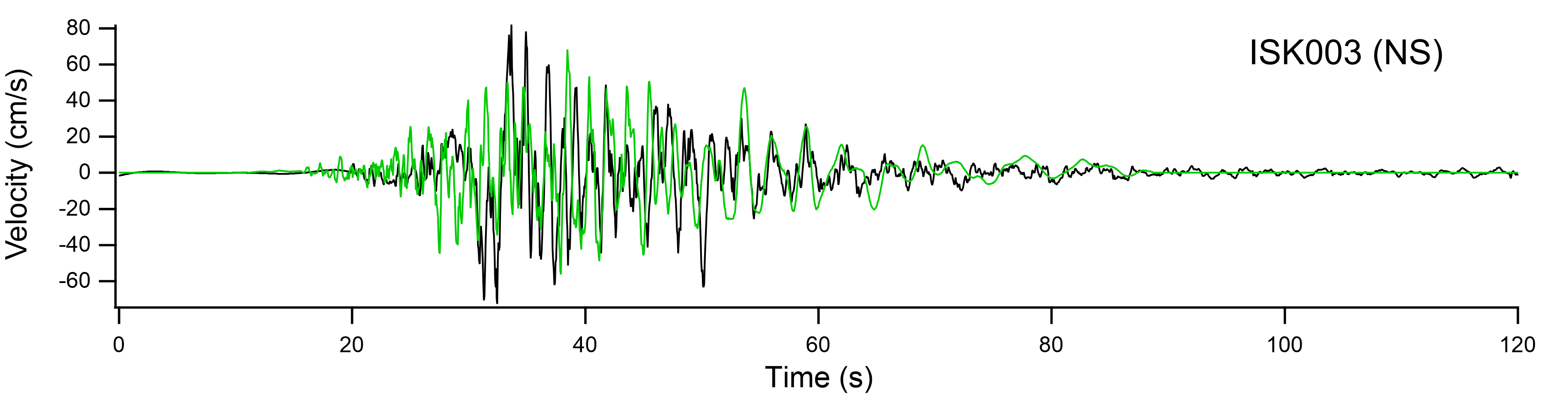
図-7　ISK003における本震波形の再現性（緑が合成波形）

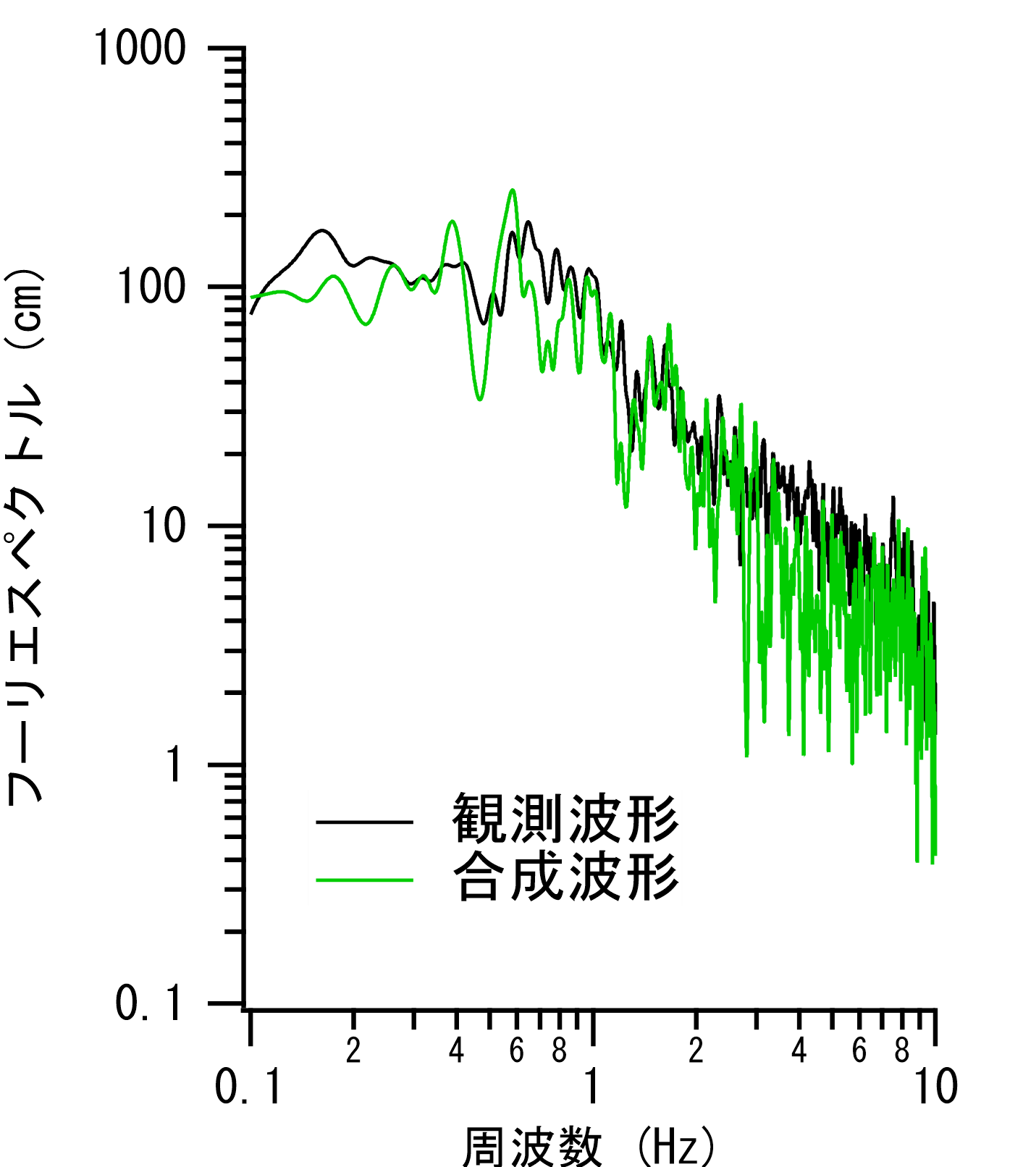
図-8　ISK003におけるフーリエスペクトルの再現性（緑が合成波形）

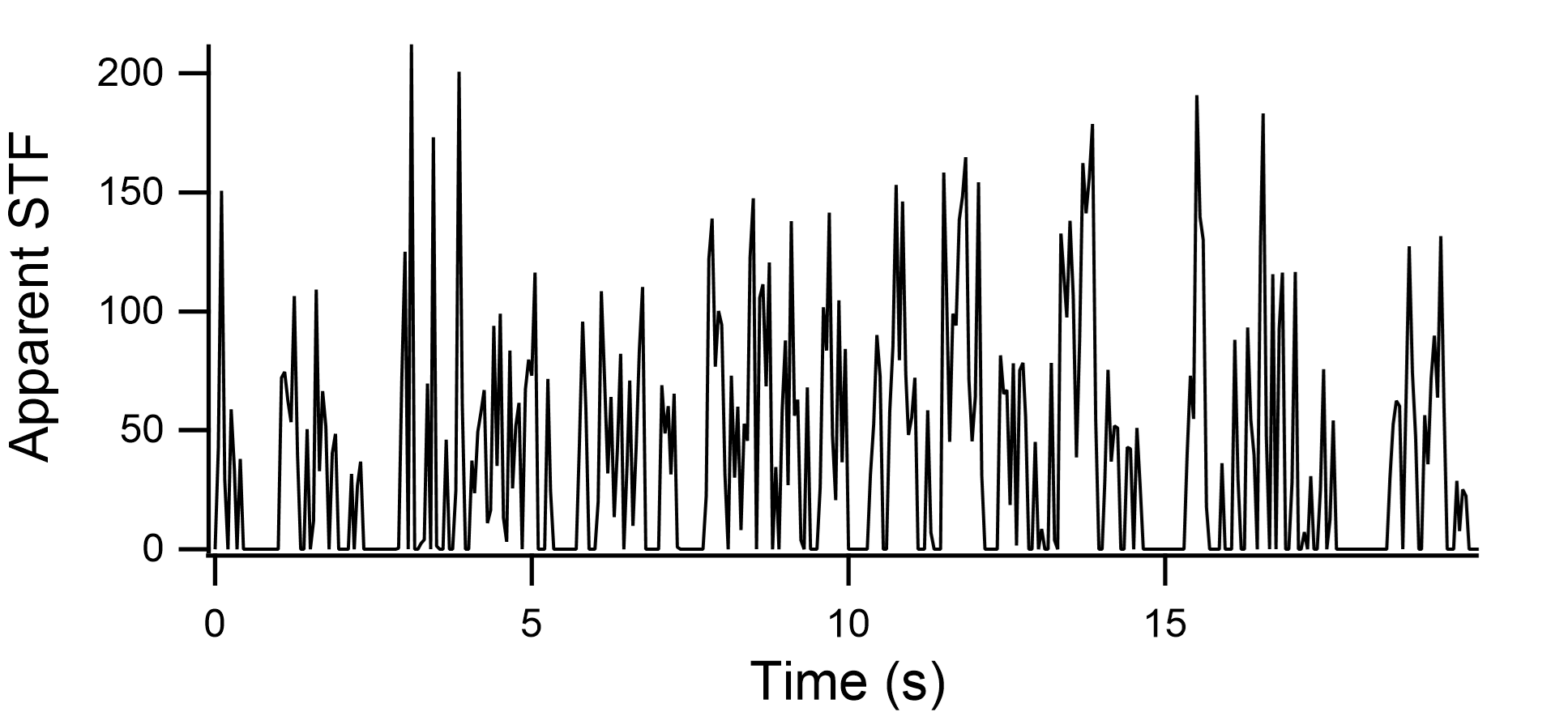
図-9　ISK003における見かけの震源時間関数

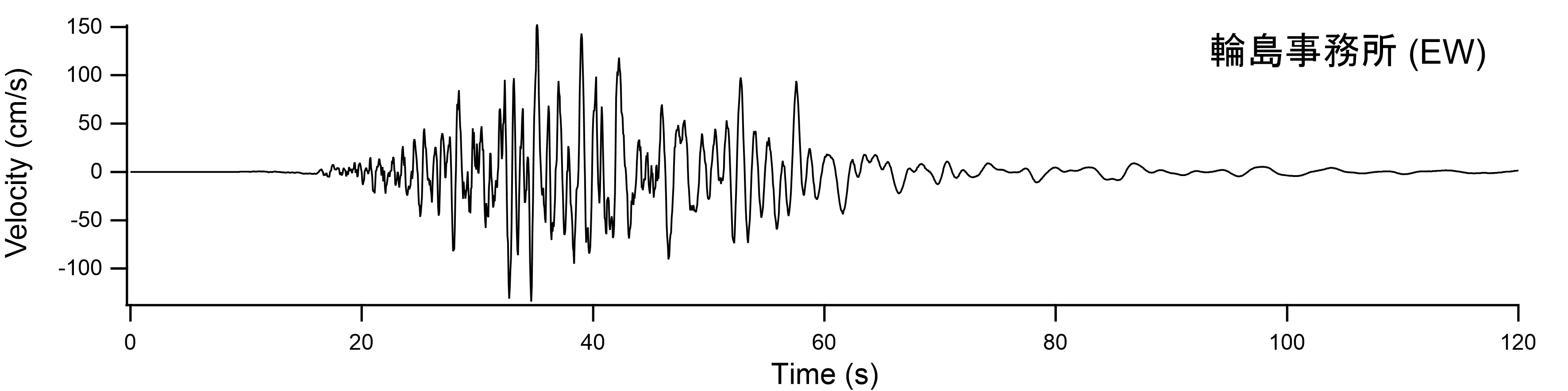
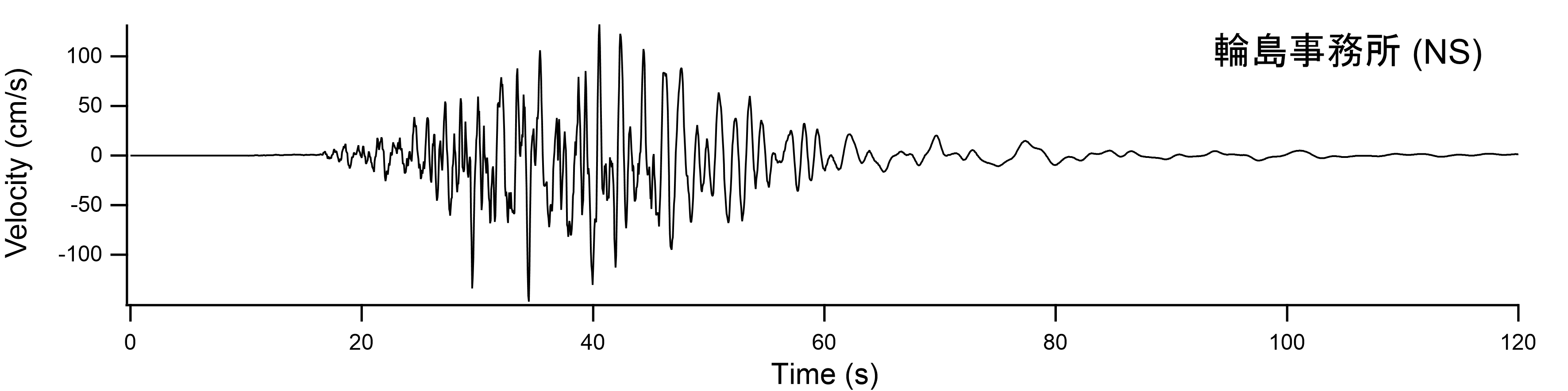
図-10　輪島港（輪島事務所）における再現波（地表における速度波形）

図-9に得られた見かけの震源時間関数を示す．これを用いて輪島港（余震観測を行った輪島事務所）における本震波形を推定した．その際，多重非線形効果を表すパラメタはISK003における波形の再現に用いたのと同じ値（ν₁=0.70，ν₂=0.02）を用いた．輪島港（輪島事務所）における再現波（地表における速度波形）を図-10に示す．PSI値はNS成分が264，EW成分が278となり，かなり厳しい地震動となった．これは，もともとISK003で観測波のPSI値がNS成分が137，EW成分が121と大きく，そこからさらに増幅があるためと考えられる．また，EW成分に関しては，「輪島港では16:10:46頃にいったん揺れが小さくなったあと16:10:54頃に2回目の大きな揺れがあった」との監視カメラ映像から読み取れる事実とある程度整合した結果が得られている．

ここで求まった地震動をL1地震動と同様の地盤モデルで工学的基盤に引き戻したものをエクセルファイルに収録した．なお，ひずみ依存曲線は北澤他³⁾のものを用いた．また，採用したν₁の値（ν₁=0.70）と整合するように，地盤の固有周波数が線形時の0.70倍を下回らないようにiterationを中途で打ち切った．