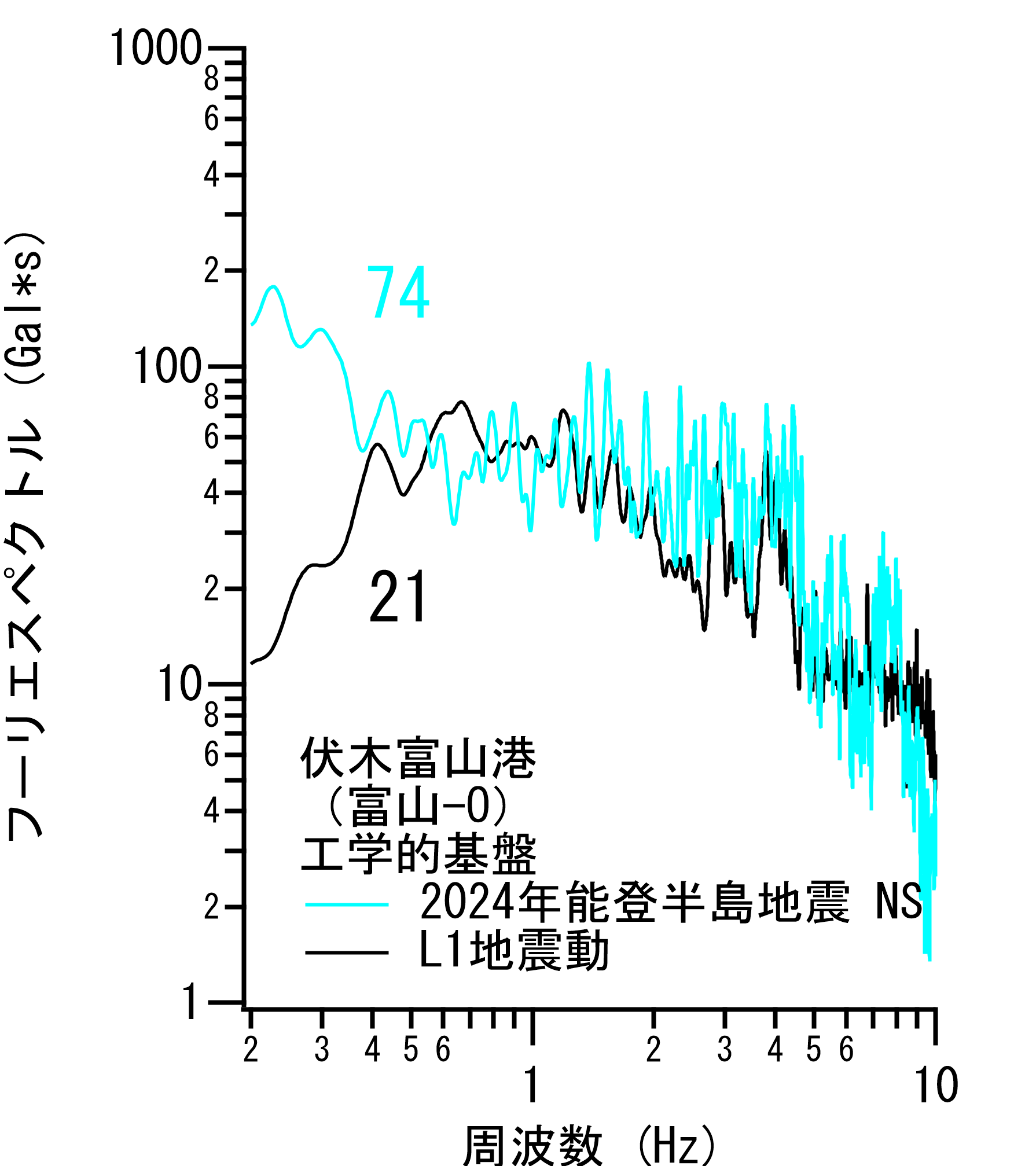
伏木富山港

伏木富山港は2024年能登半島地震（M7.6）の地震動を受けている．このとき伏木富山港の強震観測地点「富山-O」で観測された地震動を等価線形解析（FDEL）で工学的基盤の2E波に変換し，伏木富山港におけるレベル１地震動と比較した．その際，「富山-O」と同一地点である「富山-G」のサイト増幅特性を用いて設定された9317番のレベル1地震動を比較の対象とした．その結果，伏木富山港では，当該地震の地震動は，0.4Hz以上では概ねレベル1地震動相当であり，0.4Hz以下ではレベル1地震動を上回っていたと考えられる（図1）．したがってこの地震の際に存在していた施設で被害を受けなかった施設については，その後のさらなる高経年化の影響を除けば，レベル1地震動に対して十分な耐震性能を有していると判断できる．

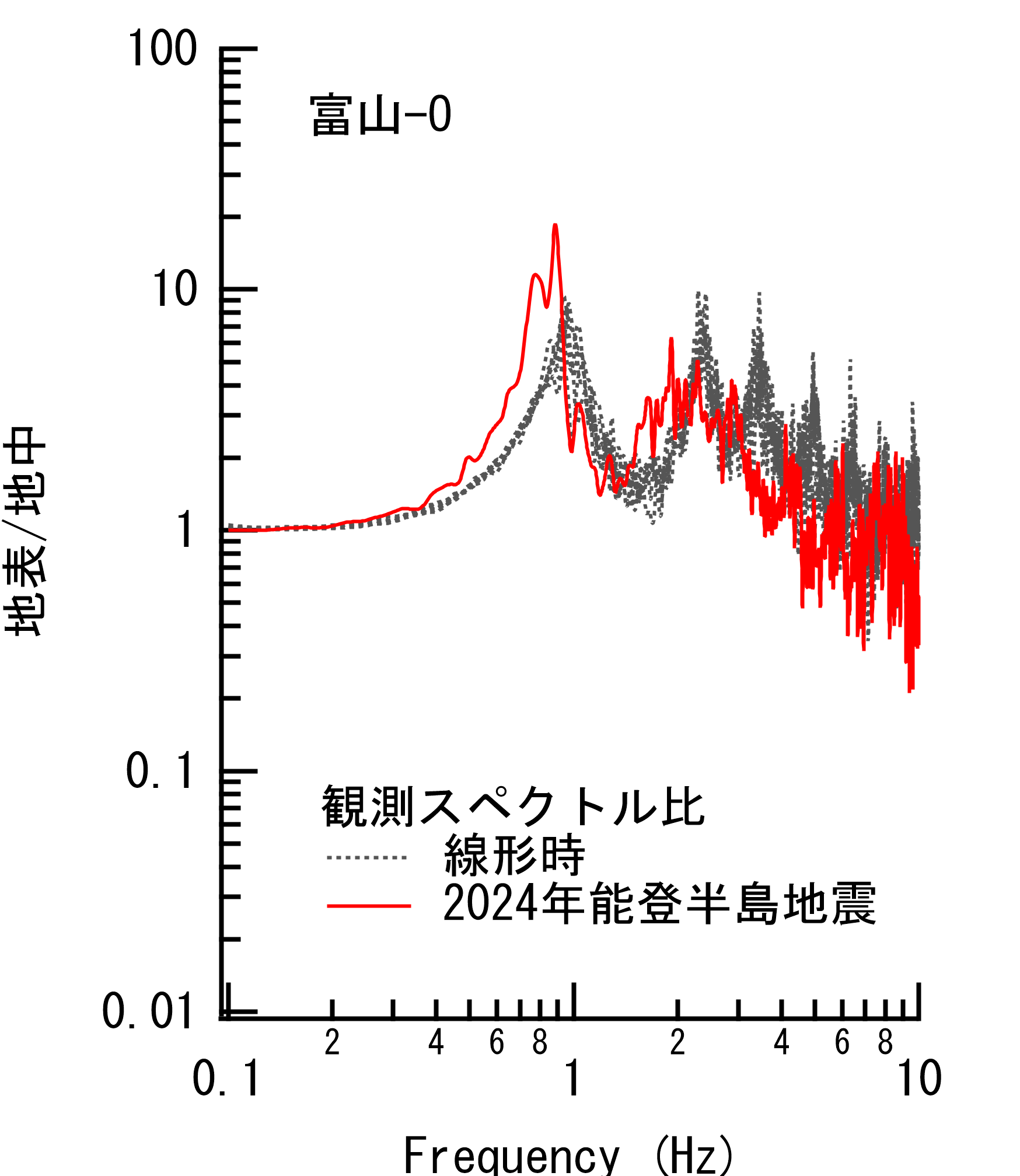
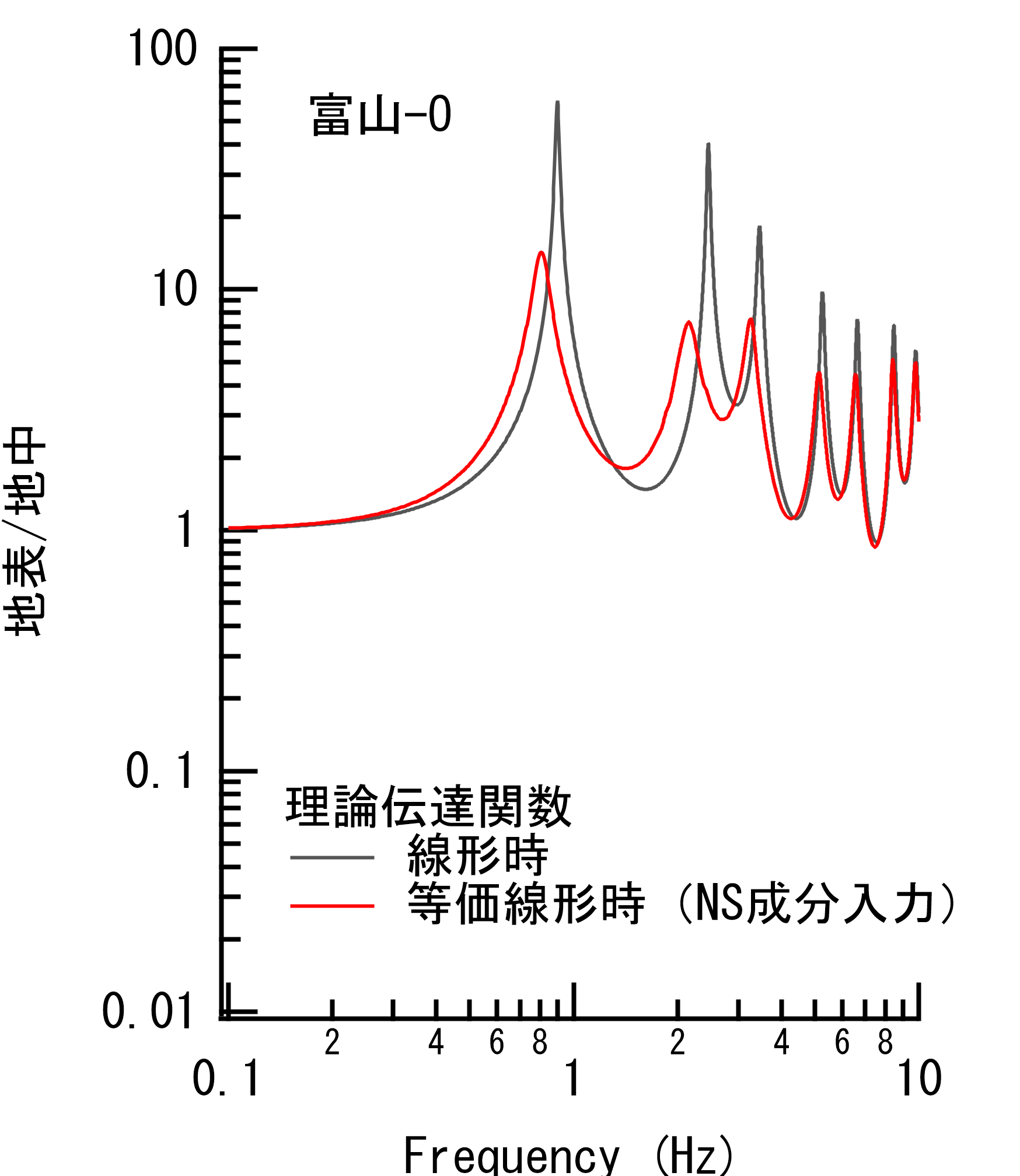
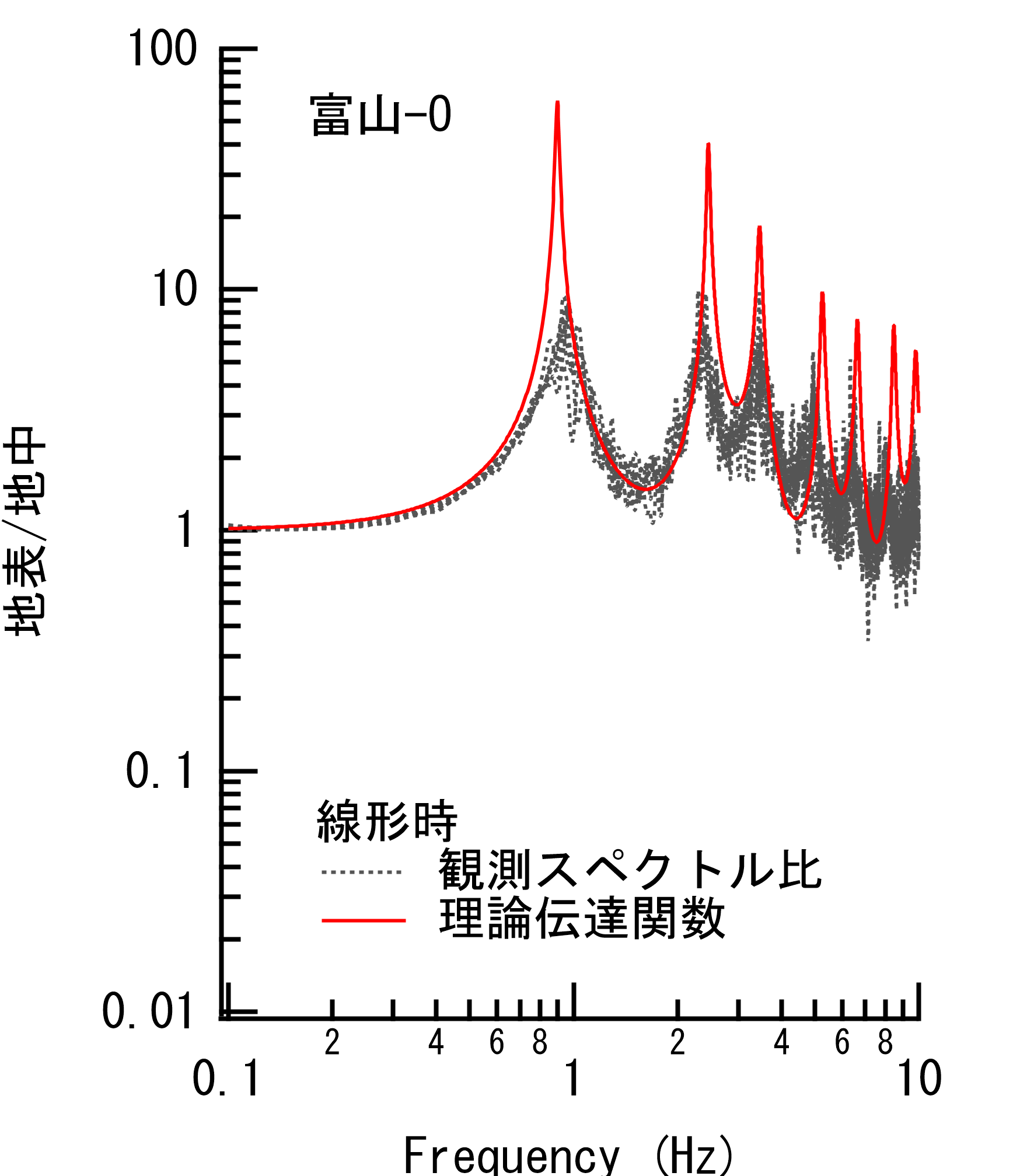
図-1　伏木富山港におけるレベル1地震動と2024年能登半島地震（M7.6）の地震動の比較．フーリエスペクトル（バンド幅0.05HzのParzenウインドウを適用）．各プロットに付与されている数字はPSI値．EW成分は欠測．

（参考情報）表1は等価線形解析に用いた地盤モデルで，強震計位置（富山-O）のボーリングデータに基づき設定した．図2は強震計位置における地表÷地中のスペクトル比で，左は観測，右は等価線形解析（FDEL）による計算結果である．観測では線形時に比べ2024年能登半島地震ではピーク周波数が低周波側に移動していることから表層地盤が非線形挙動を示していたことがわかる．等価線形解析（FDEL）ではこの傾向を表現できている．図3は同じく強震計位置における地表÷地中のスペクトル比で，線形時と非線形時のそれぞれの観測スペクトル比を理論伝達関数と比較しているが，観測スペクトル比の特徴が理論伝達関数により捉えられている．これらのことから，等価線形解析による引き戻しは適切に実施できていると判断した．

図-2　伏木富山港強震計位置（富山-O）における地表÷地中のスペクトル比．左は観測で右は等価線形解析（FDEL）による計算結果．観測では，線形時に比べ2024年能登半島地震ではピーク周波数が低周波側に移動していることから表層地盤が非線形挙動を示していたことがわかる．等価線形解析（FDEL）ではこの傾向を表現できている．

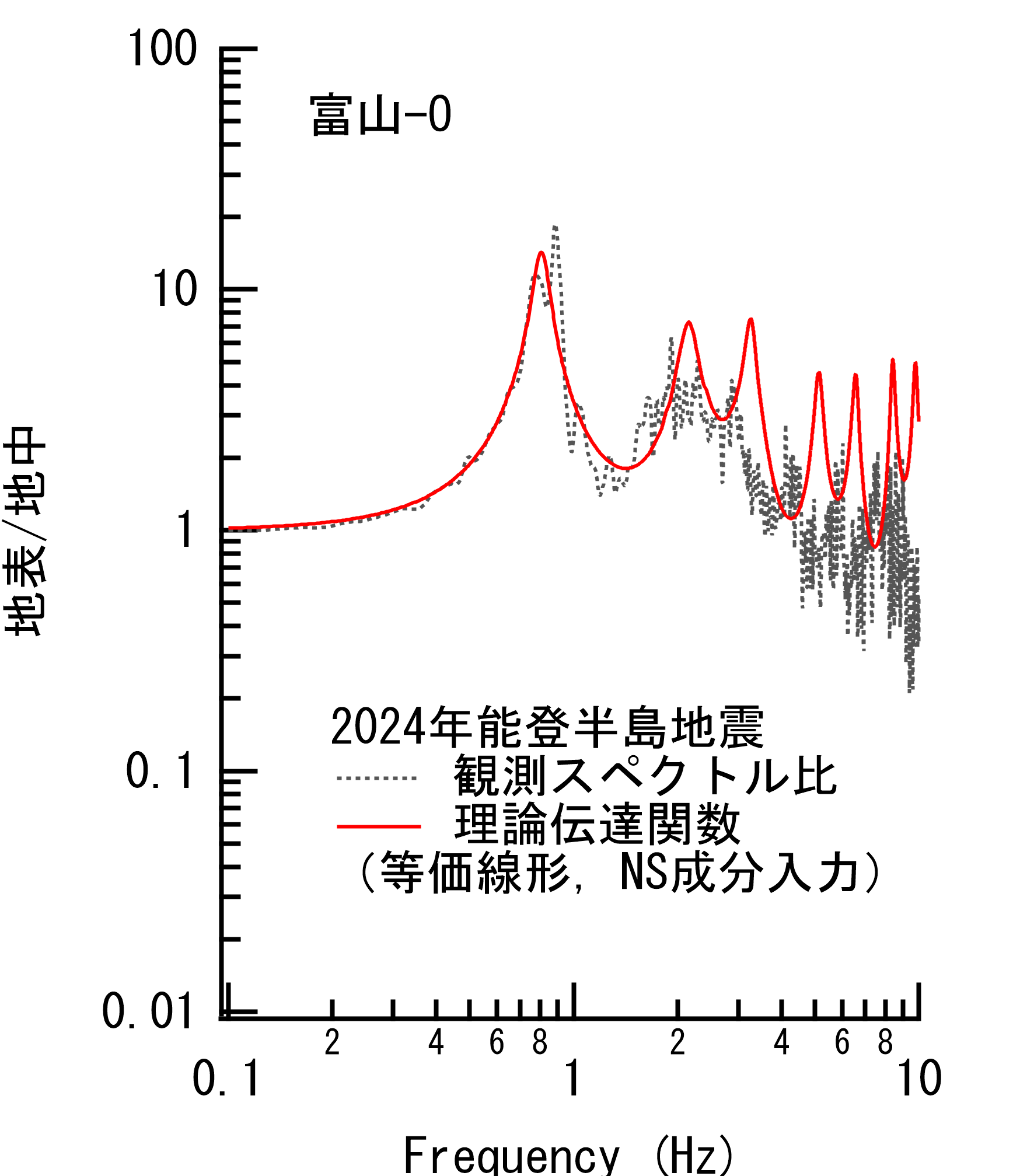
図-3　伏木富山港強震計位置（富山-O）における地表÷地中のスペクトル比．線形時と非線形時のそれぞれの観測スペクトル比と理論伝達関数の比較．